111: Begin the New Year with... an Introduction to the Poincaré Conjecture! (Pure Mathematics)

 Hey! It's been a minute since I wrote one of these, so I'm genuinely glad to be back. Happy New Year! I should be more regular now because I'm done with all university applications and I'm relatively free (as free as you can be by year 12). Today I'll be jabbering on a bit about the Poincaré Conjecture, one of the most special (solved) problems in mathematics.

The Poincaré Conjecture

Image Credit: Clay Mathematics Institute

The Poincaré Conjecture is a fundamental problem in the branch of topology, best known as one of the 7 Millennium Prize Problems of the Clay Mathematics Institute. It was one of the most famous and long-standing unsolved problems in the history of mathematics until it was finally proven in 2003 by the Russian mathematician Grigori Perelman. Perelman's proof was a monumental achievement and earned him the Fields Medal and 1 million US Dollars (from the Clay Mathematics Institute) - both of which he declined (which I'll return to later).

Henri Poincaré first proposed the conjecture in the early 20th century. Poincaré was a French polymath who made significant contributions to various branches of mathematics, physics, and philosophy.

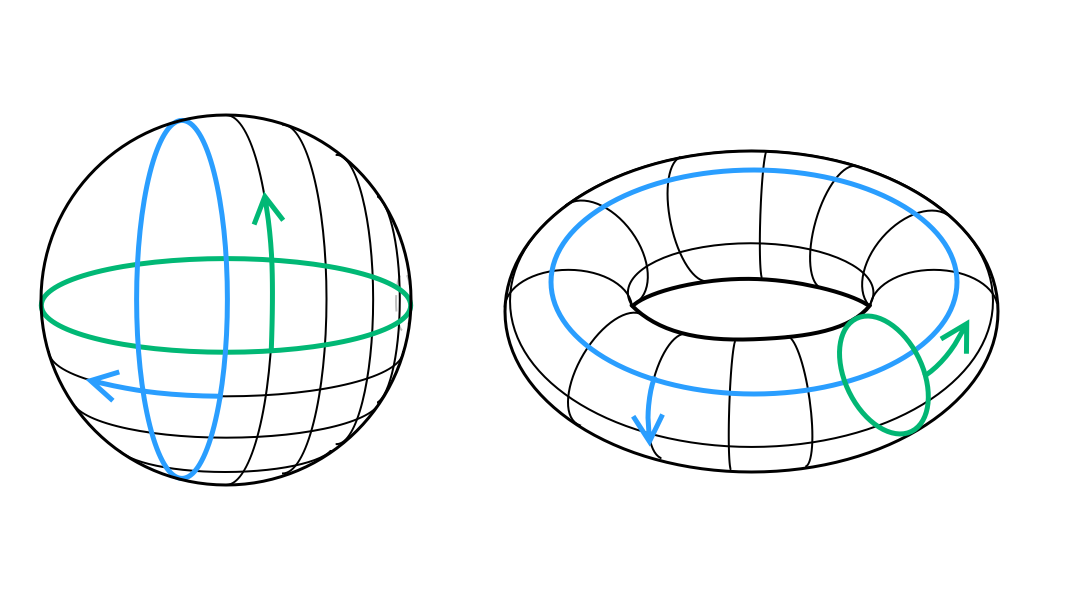
The Poincaré Conjecture deals with the topology of three-dimensional spaces. Specifically, it focuses on the classification of simply connected, closed 3-manifolds. A 3-manifold is a mathematical object that is locally similar to three-dimensional Euclidean space. "Simply connected" means that the space has no "holes" or tunnels through it. Like a bun is simply connected, but not a bagel. "Closed" indicates that the manifold is compact without any boundaries. All points can also be connected to each other.

The conjecture states that every simply connected, closed 3-manifold is topologically equivalent to a 3-dimensional sphere (a geometric object with no holes). In simpler terms, the Poincaré Conjecture asserts that any compact, simply connected, closed 3-dimensional space is essentially a 3-dimensional sphere.

For many years, the Poincaré Conjecture remained an open problem, challenging mathematicians to develop new techniques and approaches in topology. In 2003, Grigori Perelman, a Russian mathematician, published a series of papers outlining a proof of the conjecture. Perelman's proof was based on Richard S. Hamilton's theory of Ricci flow, a process that smoothens and deforms the geometry of a manifold. Perelman's work was thoroughly reviewed and verified by the mathematical community, leading to the acceptance of his proof.

Perelman's decision to decline the Fields Medal and withdraw from the mathematical community after proving the Poincaré Conjecture added a layer of mystery to the story. Nevertheless, the resolution of this long-standing problem marked a significant milestone in the history of mathematics and demonstrated the power of collaboration, perseverance, and innovation in the pursuit of mathematical knowledge. But the question remains - why did he decline the most prestigious prize in mathematics AND a million dollars?

There were 3 primary reasons - First, Perelman believed that Hamilton's work on Ricci flow was necessary to his proof, and deserved recognition too. Second, many mathematicians tried to "copy", for lack of a better word, Perelman's work - and the International Mathematical Union was considering awarding them the Fields Medal for some reason. Finally (this one more refers to the Millennium Prize), Perelman was more non-orthodox and preferred to publish his work on arXiv (a free pre-printing website) so that everyone could enjoy his work for free! However, the rules of the Millennium Prize dictated that the work should be published for 2 or more years... which isn't always comfortable for readers. A lot of people seem to ignore Perelman's REASONS for declining the awards; not that it matters, but I (personally) strongly support Dr Perelman's stance.

In my next post, I'll explain how Perelman proved the conjecture! More in layman's terms though I suppose, since my audience is primarily younger, secondary school students.

A Fun Fact: Grigori Perelman is one of my favourite mathematicians (alongside James Maynard, June Huh, Akshay Venkatesh, and Ramanujan, and others).

01001100 01101001 01110110 01100101 00100000 01001100 01101111 01101110 01100111 00100000 01100001 01101110 01100100 00100000 01010000 01110010 01101111 01110011 01110000 01100101 01110010 00100001 (No, your computer isn't hanging).

Check my profile to contact me at my e-mail address.