100: Everything You Need to Know about Newton's Method of Approximating Polynomials (Pure and Applied Mathematics)
Newton's method, also known as the Newton-Raphson method, is an algorithm used to find the roots of a polynomial function. It was developed in the late 1600s.
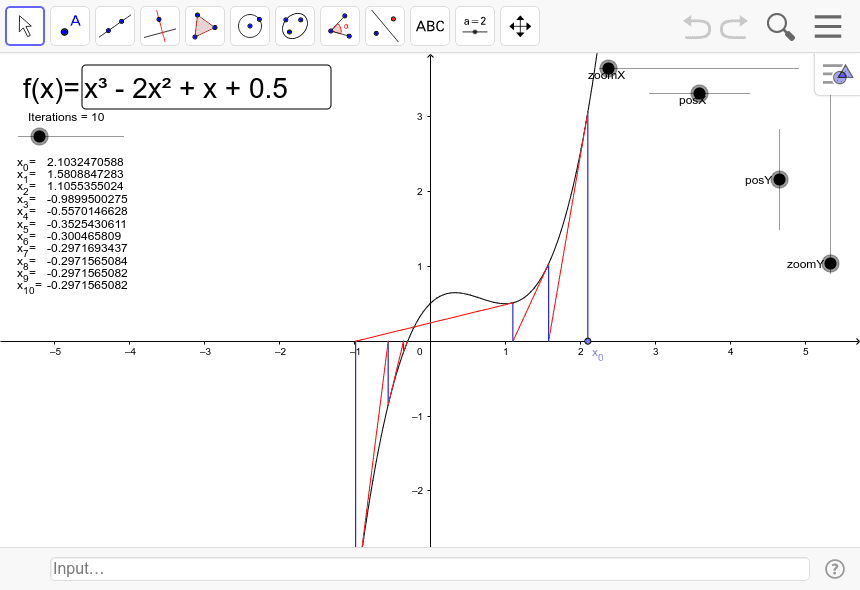
For a function f(x), finding the value of x for which f(x) = 0 is the goal of Newton's algorithm.
Here's an algorithm you can use:
Choose an initial guess for the root, let's call it x₀. Calculate the function value and its derivative at the current guess. These are denoted as f(x₀) and f'(x₀), respectively. Use the formula: x₁ = x₀ - f(x₀) / f'(x₀) to update the guess. This formula is derived from the tangent line approximation to the function at x₀, assuming it is differentiable. Repeat the last two sentences until the desired level of accuracy is achieved or until a specified number of iterations have been performed. You will know your answer is correct as the result of every iteration converges to the same value.
What to know about the algorithm:
Newton's algorithm typically converges quickly if the initial guess is close to the actual root and if certain conditions are met. However, it may fail to converge or converge to a different root if the initial guess is far from the actual root or if the function has complex behaviour near the root.
Multiple Roots: Newton's algorithm can find only one root at a time. If a function has multiple roots, you may need to apply the algorithm multiple times with different initial guesses to find each root separately.
Non-Differentiable Points: Newton's algorithm requires the function to be differentiable in the neighbourhood of the root being approximated. If the function is not differentiable at a particular point, modifications like using generalised derivatives or applying different root-finding methods may be necessary.
Slightly advanced information here:
Newton's Method for Multivariable Functions: The method can be extended to solve systems of equations or find roots of multivariable functions. In this case, the algorithm involves calculating and manipulating matrices and vectors.
The multivariable Newton's algorithm starts with an initial guess for the root vector, denoted as x₀, which is an n-dimensional vector for n variables. The update formula becomes:
x₁ = x₀ - (J⁻¹)(f(x₀))
Here, J is the Jacobian matrix, which consists of the first-order partial derivatives of the function with respect to each variable. The Jacobian matrix determines the linear approximation to the function near the current guess.
The algorithm iterates by updating the guess vector using the above formula until convergence is achieved.
Fractals: Newton's algorithm exhibits interesting behavior when applied to certain functions. Some functions may have multiple roots with different basins of attraction. A basin of attraction is the set of initial guesses that converge to a particular root. The boundaries between these basins can create fascinating fractal patterns known as Newton fractals.
By applying Newton's algorithm to complex functions, such as polynomials or transcendental equations, and visualizing the regions of convergence, intricate fractal shapes can emerge. These fractals showcase the complex dynamics and intricate relationships between different roots and initial guesses.
Optimization: Newton's algorithm can be used for optimization problems, where the goal is to find the minimum or maximum of a function. By finding the roots of the derivative of the objective function, we can locate the critical points, which can correspond to local extrema.
To apply Newton's method to optimization, the update formula becomes:
x₁ = x₀ - (f''(x₀))⁻¹(f'(x₀))
Here, f''(x₀) represents the second derivative of the objective function at the current guess x₀. This update formula converges to the local minimum or maximum depending on the properties of the function.
Alternatives: Newton's algorithm can be computationally expensive when dealing with large-scale problems due to the need to calculate and invert the Jacobian or the Hessian matrix. Quasi-Newton methods, such as the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, provide approximate solutions without explicitly computing the Hessian or its inverse.
Quasi-Newton methods iteratively update an approximation to the Hessian matrix using the function and gradient evaluations. These methods offer significant computational advantages in solving optimization problems compared to the traditional Newton's algorithm.
That's all you probably need to know as a high school student - remember this for your next math exam! (I highly doubt you'll get marks for this)
Interesting video and other resources:
https://youtu.be/iVOsU4tnouk
http://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3j/3j_2content_2.html
https://skill-lync.com/student-projects/Multivariate-Newton-Raphson-Method-03065
01001100 01101001 01110110 01100101 00100000 01001100 01101111 01101110 01100111 00100000 01100001 01101110 01100100 00100000 01010000 01110010 01101111 01110011 01110000 01100101 01110010 00100001 (No, your computer isn't hanging).
Comments
Post a Comment