110: Everything You Need to Know About the Navier-Stokes Equations (Pure Physics and Applied Mathematics)
In the intricate world of fluid dynamics, where the movement of liquids and gases forms the backdrop of countless natural phenomena, the unsolved Clay Institute Millenium Prize Problem of the Navier-Stokes equations stands as a beacon of understanding. These mathematical expressions encapsulate the intricate forces, pressures, and velocities that orchestrate the motion of fluids.
George Gabriel Stokes
Image Credit: Clay Mathematics Institute
Fluid dynamics is a captivating branch of physics and mathematics that delves into the behaviour of fluids in motion. Whether it's the ocean currents, the streams, or the turbulence in a boiling pot, understanding the principles governing fluid motion requires strong mathematical concepts and physics insights.
The Navier-Stokes equations, named in honour of the French engineer Claude-Louis Navier and the Irish mathematician George Gabriel Stokes, are the fundamental equations that explain fluid dynamics. In their general form, they can be expressed as a set of partial differential equations:
The left-hand side of the equation encapsulates two terms. The first term accounts for the change in fluid velocity over time. The second term describes the convective acceleration, reflecting the transport of fluid momentum by the fluid itself.
On the right-hand side, we find an amalgamation of terms with distinct physics significance. The first term captures the influence of pressure gradients on fluid motion. The next term is an expression of the diffusive behavior induced by viscosity, signifying the spread of momentum due to internal friction within the fluid. The final term accounts for external forces that influence the fluid, adding a layer of complexity to the equation's interpretation.
While the Navier-Stokes equations offer an explanation to the mechanics of fluid flow, their inherent complexity underscores the challenges of understanding and solving them completely. In scenarios involving turbulence—characterised by eddies—the equation's nonlinearity and coupling of various scales make obtaining analytical solutions nearly impossible.
The power of the Navier-Stokes equations extends to a multitude of domains. From optimizing the aerodynamics of aircraft wings to modeling the currents that shape our oceans and even predicting weather patterns, to research as physics competitions like the IYPT, these equations are a cornerstone for scientists and engineers seeking to unravel the mysteries of fluid motion.
As we navigate the intricacies of the Navier-Stokes equations, we embark on a journey that mirrors the complexity of fluid dynamics itself. Beyond the symbols and mathematical expressions lie the intricate symphony of forces, pressures, and velocities that govern the art of fluid flow.
In our pursuit of understanding fluids, we encounter not just equations, but a profound appreciation for the physics that orchestrates the beauty and chaos that fluid dynamics offers.
Hey again! This is Shikhar. Thanks for reading this post. This is likely to be my last post in a while since my year 12 midterm exams are about to start and I'll be filling in applications soon after. I'll be back around January or February with a new post. Until then, live long and prosper!
01001100 01101001 01110110 01100101 00100000 01001100 01101111 01101110 01100111 00100000 01100001 01101110 01100100 00100000 01010000 01110010 01101111 01110011 01110000 01100101 01110010 00100001 (No, your computer isn't hanging).
Check my profile to contact me at my e-mail address.

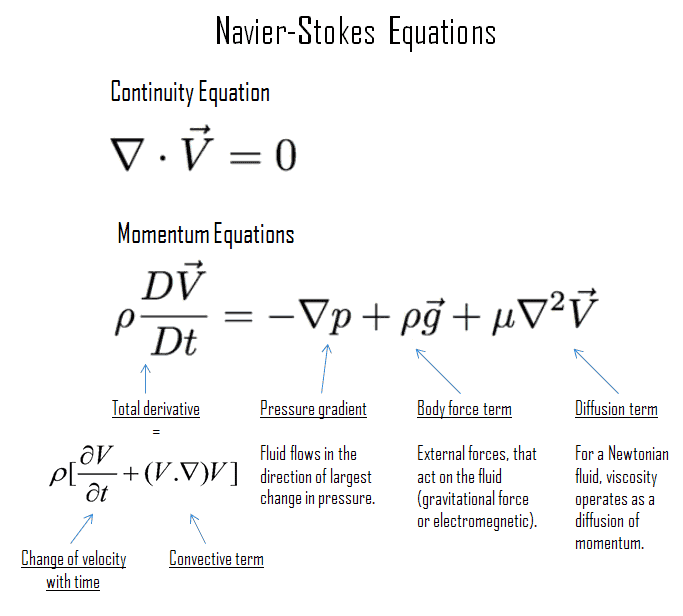
Comments
Post a Comment